Crypto_RSA算法总结

Crypto

Word count: 1.6kReading time: 6 min

 2018/05/18 

最近比赛过多，没来得及总结，web已经很难突破了，学一波Crypto吧。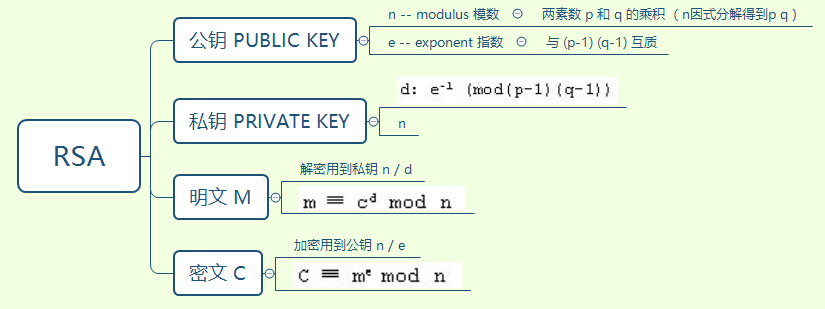
rsa

RSA算法简介：
CTF中的RSA题型
RSA的常见攻击方法
CTF中RSA的一些题目
- 在一次RSA密钥对生成中，假设p=473398607161，q=4511491，e=17，求d
- c 是密文已知 p、q、e 求明文.

个人做题总结：
1.当e过大时，用Wiener attack

RSA算法简介：

RSA算法涉及三个参数，n，e，d，私钥为（n，d），公钥为（n，e）。

其中n是两个大素数p，q的乘积(n=p*q)。c为密文，m为明文。

d和e互为模反元素，φ(n)是n的欧拉函数(φ(n)= φ(p×q)=φ(p)φ(q)=(p-1)(q-1))。
φ = (p−1) * (q−1) 即n的欧拉函数，然后选择一个e (1<e<φ)，且e和φ互质
取e的模反数为d，计算方法:e * d ≡ 1 (mod φ)

对明文m进行加密：*c = pow(m, e, N)*，得到的c即为密文

对密文c进行解密，*m = pow(c, d, N)*，得到的m即为明文

加密：c=m^e mod n

解密：m=c^d mod n

总结：

 p 和 q ：大整数N的两个因子（factor）

 n：大整数n，我们称之为模数（modulus)

 e 和 d：互为模反数的两个指数（exponent）

 c 和 m：分别是密文和明文，这里一般指的是一个十进制的数。

CTF中的RSA题型

CTF中的RSA题目一般是将flag进行加密，然后把密文（即c）和其他一些你解题需要的信息一起给你，你需要克服重重难关，去解密密文c，得到flag（即m），一般有下列题型。

公钥加密文
这是CTF中最常见最基础的题型，出题人会给你一个公钥文件（通常是以.pem或.pub结尾的文件）和密文（通常叫做flag.enc之类的），你需要分析公钥，提取出（N，e），通过各种攻击手段恢复私钥，然后去解密密文得到flag。

文本文档
对于第一种题型，耿直点的出题人直接给你一个txt文本文档，里面直接写出了（N，e，c）所对应的十进制数值，然后你直接拿去用就行了。当然也不都是给出（N，e，c）的值，有时还会给出其他一些参数，这时就需要思考，这题具体考察的什么攻击方法

pcap文件

有时出题人会给你一个流量包，你需要用wireshark等工具分析，然后根据流量包的通信信息，分析题目考察的攻击方法，你可以提取出所有你解题需要用到的参数，然后进行解密

本地脚本分析

题目会给你一个脚本和一段密文，一般为python编写，你需要逆向文件流程，分析脚本的加密过程，写出对应的解密脚本进行解密

远程脚本利用

这种题型一般难度较大。题目会给你一个运行在远程服务器上的python脚本和服务器地址，你需要分析脚本存在的漏洞，确定攻击算法，然后编写脚本与服务器交互，得到flag.

RSA的常见攻击方法

当模数N过小时

RSA的非对称体制是建立在大整数分解难题上的，所以最基本的攻击方法就是当模数N过小时，我们可以写个脚本直接爆破他的因子，如
N = 1211809

for i in range(2, N):

    if N % i == 0:

        print i

在CTF中出现的不会太小，一般是不可能爆破分解的，都是要用到一些攻击算法的。

分解大整数的一些算法

Wiener’s attack

https://en.wikipedia.org/wiki/Wiener%27s_attack

使用:当d < (1/3) N^(1/4)时

费马分解

当大整数N的两个因子p和q相近时

Small q

当q较小时，即|p-q|较大时，我们可以直接爆破因子

Boneh Durfee Method

当d满足 d ≤ N^0.292 时，我们可以利用该方法分解N，理论上比wiener attack要强一些。

yafu

yafu使用最强大的现代算法去自动化的分解输入的整数。大多数的算法都实现了多线程，让yafu能充分利用多核处理器（算法包括 SNFS, GNFS, SIQS, 和 ECM）。

factordb

如果对一个大整数用一些特殊算法也分解不了的时候，我们可以在 http://factordb.com/ 中查询一下数据库，说不定就能找到其因子

其他一些题型

有些题会给你一些随机生成的大整数，一般来说是无法直接分解的，不过一般会给我们其他切入点

Rabin算法

当e等于2时

小公钥指数攻击

当e十分小时，比如e等于3时

d泄露攻击

如果我们知道一组过期的（N，e1，d1）和一组由新的e2组成的公钥及其加密的密文（N，e2，c），我们可以由（e1，d1）得到模数N的两个因子p和q，再去算e2的模反数d2，去解密密文

共模攻击

使用相同的模数 N 、不同的私钥，加密同一明文消息

模不互素

两个公钥的N不互素时

Known High Bits Factor Attack

我们知道模数N其中一个因子的高比特位时

Stereotyped messages

如果你知道明文中最重要的部分，您可以使用此方法找到消息的其余部分。

Basic Broadcast Attack

同一个加密指数e和不同且互素的模数N加密了同一个密文，并发送给了其他e个用户

CTF中RSA的一些题目

在一次RSA密钥对生成中，假设p=473398607161，q=4511491，e=17，求d

http://www.shiyanbar.com/ctf/1828

# coding=utf-8
import gmpy2

p = 473398607161
q = 4511491
e = 17

phi = (p - 1) * (q - 1)
# 计算得到私钥（n, d）
d = long(gmpy2.invert(e, phi))
print d

c 是密文已知 p、q、e 求明文.

http://www.shiyanbar.com/ctf/1979

import gmpy2

p = 9648423029010515676590551740010426534945737639235739800643989352039852507298491399561035009163427050370107570733633350911691280297777160200625281665378483L

q = 11874843837980297032092405848653656852760910154543380907650040190704283358909208578251063047732443992230647903887510065547947313543299303261986053486569407L

e = 65537L

c= 83208298995174604174773590298203639360540024871256126892889661345742403314929861939100492666605647316646576486526217457006376842280869728581726746401583705899941768214138742259689334840735633553053887641847651173776251820293087212885670180367406807406765923638973161375817392737747832762751690104423869019034L

phi = (p - 1) * (q - 1)

# 计算得到私钥（n, d）

d = long(gmpy2.invert(e, phi))

n = p * q

# 计算并输出c^d mod n

print pow(c, d, n)